Ovládání času - technologie a metody (2)
Cestování téměř rychlostí světla
Cestování téměř rychlostí světla má schopnost výrazně roztáhnout čas, čímž pošle akcelerujícího cestovatele rychle kupředu v čase v poměru s těmi, kteří zůstali pozadu.
Čím blíže rychlosti světla, tím dále do budoucnosti.

Klíčové charakteristiky použití cestování téměř rychlostí světla pro ovládání času a cestování v čase jsou uvedeny na obrázku níže.

Počítačová simulace proudu fotonů a elektronů cestujících rychlostí rovnající se 98% rychlosti světla, při čemž naráží do mezihvězdného materiálu a mísí se s ním.
Alcubierrův warpový pohon
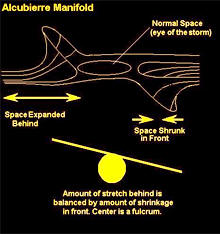
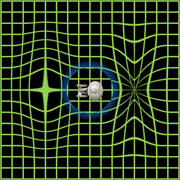
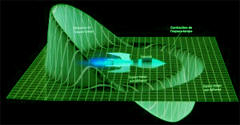
Alcubierrův warpový pohon natahuje prostoročas ve vlně a způsobuje, že struktura prostoru před kosmickou lodí se smršťuje a prostor za ní se roztahuje.
Loď se může „vézt“ na vlně k akceleraci do vysokých rychlostí a cestování v čase.

Alcubierrův pohon, známý také pod pojmy Alcubierrova metrika či warpový pohon, je matematický model prostoročasu vykazující rysy připomínající smyšlený „warpový pohon“ ze Star Treku, který může cestovat „rychleji než světlo“ (i když ne v místním slova smyslu – viz níže).
Klíčové charakteristiky použití Alcubierrova warpového pohonu pro ovládání času a cestování v čase jsou vedeny na obrázku níže.

Popis Alcubierrova warpového pohonu
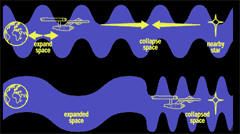
V roce 1994 navrhl mexický fyzik Miguel Alcubierre metodu natahování prostoru ve vlně, což by teoreticky způsobilo, že by se struktura prostoru před kosmickou lodí smršťovala a za ní roztahovala.
Loď by se pak „vezla“ na této vlně uvnitř oblasti známé pod pojmem warpová bublina plochého prostoru. Protože loď se v bublině nepohybuje, ale je nesena při pohybu samotné oblasti, nevztahují se na ni konvenční relativistické efekty takovým způsobem, jakým by to bylo v případě, že by se loď pohybovala velkou rychlostí plochým prostoročasem.
Tato metoda cestování se v lokálním smyslu ve skutečnosti netýká pohybu rychlejšího než světlo, protože světelný paprsek v bublině se bude vždy pohybovat rychleji než loď; je to „rychlejší než světlo“ pouze v tom smyslu, že díky smršťování prostoru před lodí, může loď dosáhnout svého cíle rychleji než světelný paprsek, který musí cestovat mimo warpovou bublinu.
Proto Alcubierrův pohon neodporuje konvenčnímu tvrzení, že relativita nedovoluje, aby objekt pomalejší než světlo akceleroval na rychlost vyšší než je rychlost světla.
Alcubierrova metrika
Alcubierrova metrika definuje takzvaný prostoročas warpového pohonu.
Toto je Lorentzova varieta, která, je-li interpretována v kontextu obecné relativity, vykazuje rysy připomínající warpův pohon ze Star Treku: warpová bublina se objevuje ve dříve plochém prostoročasu a dává se do pohybu nadsvětelnou (superluminální) rychlostí. Obyvatelé bubliny nepociťují žádné účinky setrvačné síly. Objekt(y) uvnitř bubliny se nepohybují (lokálně) rychleji než světlo, místo toho se prostor okolo nich posouvá, takže objekt(y) dorazí do své destinace rychleji, než by dorazilo světlo v normálním prostoru.
Alcubierre vybral pro funkci f specifickou formu, ale jiné možnosti dávají jednodušší prostoročas vykazující požadované účinky „warpového pohonu“ jasněji a jednodušeji.
Matematika Alcubierrova pohonu
Použitím formalizmu 3+1 obecné relativity je prostoročas popsán štěpením prostoru podobných hyperploch neměnné souřadnice času t. Obecná formulace Alcubierrovy metriky je:
![]()
kde α je funkce ztráty, která udává interval vlastního času mezi nejbližšími hyperlochami;
βi je vektor posuvu, který dává do poměru prostorové soustavy souřadnic různých hyperploch;
a γij je kladně definitní metrika na každé hyperploše.
Konkrétní formulace, kterou Alcubierre studoval je definována:
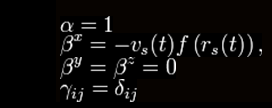
kde
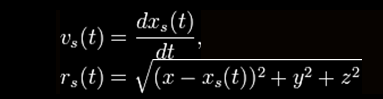
a
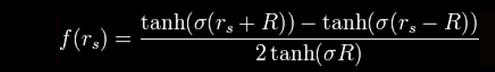
s volnými parametry R > 0 a σ > 0. Alcubierrovovu specifickou formulaci metriky lze tedy zapsat jako:
![]()
S touto konkrétní formulací metriky lze ukázat, že hustota energie měřená pozorovateli, jejichž čtyřvektor rychlosti je vůči hyperplochám normální, je udán
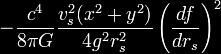
kde g je determinant metrického tenzoru. Tudíž protože hustota energie je záporná, potřebuje člověk k cestování rychlostí vyšší než je rychlost světla exotickou hmotu.
Existence exotické hmoty není teoreticky vyloučena. Navrhovanou existenci takovéto hmoty podporuje Casimirův efekt i zrychlující vesmír.
Avšak vyrobení dostatečného množství exotické hmoty a udržovat ji v takovém stavu, aby podávala zvláštní výkony, jako je např. cestování rychlostí větší než rychlost světla (a také udržovat otevřené „hrdlo“ červí díry), je považováno za neproveditelné.
Umírnění jedinci tvrdili, že v kontextu obecné relativity je nemožné sestrojit warpův pohon při absenci exotické hmoty.
Všeobecně se má za to, že konzistentní teorie kvantové gravitace vyřeší tyto otázky jednou provždy.
Fyzika Alcubierrova pohonu
Pro ty z vás, kdo jsou obeznámeni s účinky speciální relativity, jako Lorentzovo smršťování a dilatace času, má Alcubierrova metrika zdánlivě zvláštní aspekty.
Konkrétně Alcubierre ukázal, že i když loď zrychluje, cestuje na geodetické čáře volného pádu. Jinými slovy, loď využívající warpův pohon k akceleraci a zpomalení je vždy ve volném pádu a posádka nepocítí žádné akcelerační gravitační síly (přetížení).
Enormní přílivové síly budou přítomny poblíž hranic objemu plochého prostoru, kvůli velkému zakřivení prostoru, ale vhodnou specifikací by v objemu, který zabírá loď, byly zmenšeny na velmi malou hodnotu.
Původní metrika warpova pohonu, a její jednoduché varianty, mají ADM formalizmus (Hamiltonova formulace obecné relativity, vyvinuli Arnowitt, Deser a Misner, pozn. překl.), který se často používá při diskutování o prvotní hodnotě formulace obecné relativity. Toto může vysvětlovat rozšířené mylné pojetí, že tento prostoročas je řešením polní rovnice obecné relativity. Metriky v ADM formalizmu jsou přizpůsobené jisté soustavě inerciálních pozorovatelů, ale tito pozorovatelé nejsou ve skutečnosti fyzicky odlišení od jiných takovýchto soustav.
Alcubierre pojal svou „warpovou bublinu“ pomocí smršťování „prostoru“ před bublinou a jeho expanzí za ní. Ale tento výklad může být zavádějící, protože smršťování a rozšiřování se ve skutečnosti vztahuje na relativní pohyb blízkých členů ADM pozorovatelů.
V obecné relativitě člověk nejprve specifikuje přijatelné rozložení hmoty a energie, a pak zjistí geometrii prostoročasu, která je s tím spojená; ale je také možné použít Einsteinovy rovnice opačným směrem, nejprve určit metriku a pak zjistit tenzor energie-hybnosti, který je s ní spojený. A právě toto udělal Alcubierre při budování své metriky.
Tento postup znamená, že řešení může porušit různé energetické podmínky a vyžadovat exotickou hmotu.
Potřeba exotické hmoty vede k otázkám o tom, zda je vlastně možné nalézt způsob distribuce hmoty v prvotním prostoročasu, v němž není „warpová bublina“, takovým způsobem, aby byla bublina vytvořena později. Avšak ještě dalším problémem je, že podle Sergeje Krasnikova by bylo nemožné vytvořit bublinu bez toho, abychom byli schopni přinutit exotickou hmotu k tomu, aby se lokálně pohybovala rychlostí větší než je rychlost světla, což by vyžadovalo existenci tachyonů.
Byly navrhovány některé metody, které by se vyhnuly problému s pohybem tachyonů, ale před bublinou by pravděpodobně vytvořily holou singularitu.
Obtíže
Závažné problémy s metrikou tohoto formalizmu vycházejí z faktu, že veškeré známé prostoročasy warpového pohonu porušují různé energetické podmínky.
Je pravda, že určité experimentálně potvrzené kvantové jevy, jako je např. Casimirův efekt, pokud je popsán v kontextu teorií kvantového pole, vedou k napěťovým tenzorům, které rovněž porušují energetické podmínky, a tak může člověk doufat, že Alcubierrův typ warpového pohonu by možná mohl být fyzikálně proveditelný, kdyby se využilo takovýchto kvantových efektů.
Nicméně pokud určité kvantové nerovnosti předpokládané Fordem a Romanem trvají, pak mohou být energetické nároky některých warpových pohonů absurdně gigantické, např. by mohla být zapotřebí energie rovnající se 1067 gramům k přepravení malé kosmické lodi přes Mléčnou dráhu. Toto jsou řádové hodnoty vyšší, než je hmota vesmíru.
Byly nabídnuty protiargumenty vůči těmto zdánlivým problémům, ale ne všichni jsou přesvědčeni, že je lze překonat.
Chris Van Den Broeck se v roce 1999 pokusil zabývat potenciálními problémy.
Smrštěním 3 +1 dimenzionální plochy povrchu „bubliny“ přepravované pohonem, a současným rozšířením třídimenzionálního objemu obsaženého uvnitř, byl Van Den Broeck schopný snížit celkovou energii potřebnou k přepravě malých atomů na více než 3 sluneční hmotnosti (solar mass M☉= 1,98892×1030 kg, pozn. překl.). Později, mírnou úpravou Van Den Broeckovy metriky , Krasnikov snížil nezbytné celkové množství negativní energie na několik málo miligramů.
Krasnikov navrhl, že pokud by tachyony nemohly být nalezeny nebo použity, pak by mohlo být řešením zpracovávat hmoty podél trajektorie plavidla tak, aby bylo vyrobeno požadované pole. Ale v tomto případě není plavidlo s Alcubierrovým pohonem schopno pohybovat se po galaxii podle své vůle.
Je schopno pohybovat se pouze po trasách, které byly, stejně jako železnice, předtím vybaveny potřebnou infrastrukturou.

Miguel Alcubierre
Pilot uvnitř bubliny je příčinně oddělen od jejích stěn a nemůže provádět žádné operace mimo bublinu.
Nicméně je nezbytné podél trasy předem umístit zařízení, a protože pilot to nemůže provést během „přenosu“, nelze bublinu využít pro první cestu ke vzdálené hvězdě. Jinými slovy, aby člověk cestoval na Vegu (která je 26 světelných let od Země), musí nejprve všechno uspořádat tak, aby se objevila bublina pohybující se k této hvězdě nadsvětelnou rychlostí, a to bude vždycky trvat déle než 26 let.
Coule argumentoval, že scénáře, jako je ten navrhovaný Alcubierrem, jsou neproveditelné, protože hmota, která má být předem umístěna na cestě, musí být umístěna nadsvětelnou rychlostí. Proto je podle Couleho třeba Alcubierrova pohonu, aby vytvořil Alcubierrovu cestu. Jelikož ještě nebylo dokázáno, že by to existovalo, je nemožné pohon sestrojit, i když je metrika fyzikálně smysluplná.
Coule argumentuje, že podobná námitka bude platit pro jakoukoliv navrhovanou metodu na sestrojení Alcubierrova pohonu.
-pokračování-(c)2010 Translation: Lenka Hauke


