Geometrie vesmírného prostoru jinak (2) - Jiný prostor Vesmíru před očima

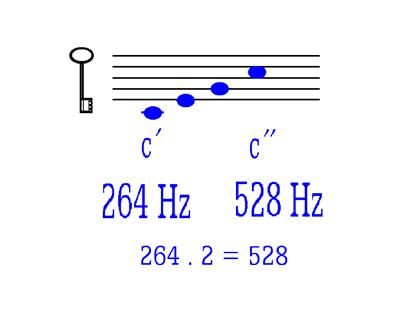
         Ten obor poznání je vyspělý, vědecky obhajitelný, jehož výsledky lze výpočetně prokázat. Splňuje to dokonce i hudba - pro akordy a stupnice platí známé matematické vztahy (obr. 1). Nerad slyším nedokončenou stupnici ze sedmi tónů. V mém požadavku uslyšet i ten poslední tón celé oktávy mě podporuje matematika. Poslední tón má dvojnásobný kmitočet proti prvnímu. Nesplnění poměru 2:1 nevede k příjemnému pocitu. Jestliže plošnému útvaru - čtverci nelze přiřadit racionální délku úhlopříčky podle výpočtu Pythagorovou větou, pak nemůžu být spokojený. Euklidův lineární spojitý prostor není matematizovatelný. Užívaný prostor si nesmlouvavě žádá kvadratickou rovnici a2 + a2 = u2. Ale výpočetní postup pak nevede k racionálnímu řešení. Kolem řešení můžeme vytvářet ledacos (obr. 2). Rozhodující je, že výpočet nekončí - jednotkovému čtverci nevyjde žádná délka úhlopříčky. Tvrdím opovážlivě - přestaňme týrat matematiku! Jak délku získat a bez zaokrouhlení? Vůči Euklidovu lineárnímu spojitému prostoru s jeho iracionalitami mám i další, zdánlivě legrační výhradu: nikdo nikdy ho neviděl.

Obr.2

        2. Matematizace nelineárního prostoru

        Popsal jsem, že se neosvědčuje spojení: lineární prostor + kvadratická rovnice. Tudíž souvislosti převrátím.

        Zaměním obě podstaty a zvolím: kvadratický prostor + lineární rovnice. Kvadraticky stlačený prostor je mně povědomý. Zjišťuji v něm prostor s perspektivou, který ve svém vědomí přisuzujeme zraku. Fyzika málo dbá vysvětlení tohoto perspektivního prostoru (obr. 3). Nedoporučuji cejchovat svět lineárním měřítkem.

Obr.3

        Kulový prostor, v němž ubývá rozměrů od středu koule k jejímu povrchu, studoval Hermann Helmholtz v 19. století.

       3. Matematika zrakového prostoru

       Mechanický model prostoru stlačeného perspektivou popíšu větami:

       Délkové měřítko osy, v jejímž počátku se nachází pozorovatel, je očíslováno celými čísly. Rysky na ose jsou rozmístěné lineárně, ale jejich cejchování se mění kvadraticky. (obr.4)

Obr.4

       Hustota informací o předmětě závisí na jeho vzdálenosti od pozorovatele. Zmenšováním vzdalovaného předmětu informací o něm ubývá. Oko získá z jednotky délky méně údajů. Hvězdu na nebi vidíme jako bod, ačkoliv je obrovská.

       Zhuštění nablízku je výhodné: blízkým předmětům ať tvor vidí podrobnosti (obr. 5). Vzdálenější věci jich mají méně, protože pro svou vzdálenost jsou mu málo potřebné a méně nebezpečné. I v tomto se konstrukce světa jeví promyšlenou a tím splňuje známou touhu Alberta Einsteina.

Obr.5

        4. Důvěryhodnost kvadratického prostoru

       Ověřuji, který ze spojitých prostorů je věrohodnější - zda lineární nebo kvadratický.

       V lineárním prostoru výpočet souřadnice bodu A, ležícího na kružnici o poloměru r = 2, vyžaduje kvadratickou rovnici x2 + y2  = r2 (obr. 6). Výpočet vede k iracionálnímu výsledku. Podle povolené nepřesnosti získáme souřadnici svislé osy yA až zaokrouhlením nevypočítatelné hodnoty.

Obr.6

           V kvadratickém prostoru lze vypočítat racionální souřadnici bodu A (obr. 7). I tentokrát leží na stejné kružnici. Používám kvadratické měřítko na obou osách 2D prostoru a proto je její poloměr r = 4. Je odlišný od poloměru v lineárním prostoru. Užitím lineární rovnice x + y = r vychází racionální výsledek yA = 3.

    Obr.7

        Při ověřování obou prostorů lze posuzovat zrakové zážitky (obr. 8). Velikost sloupků ve zrakovém zážitku je určená zorným úhlem. Ten je vyjádřen na I. sloupku. Když pak zvolím zobrazení v kvadratickém prostoru (obr. 9), zjišťuji ten samý zorný úhel.

Obr.8

Obr.9

       Sloupky II., III. a IV. nakreslené čárkovaně - jsou skutečné, nebo pouze máme pocit ve shodě s Euklidovým názorem, že takový svět je? Které sloupky nakreslené plnou čarou jsou důvěryhodné? O skutečnosti jednoho nebo druhého řešení rozhoduje matematizace.

       Zjišťuji, že prostor, který nám představuje zrak, je matematizovatelný! Nepotřebuje iracionální čísla pro vyjádření vzdáleností.

       V kvadratickém prostoru platí pro rovnoramenný trojúhelník lineární rovnice (obr. 10). Je to předělávka Pythagorovy věty; získala tvar a +b = c.

Obr.10

        Navíc i další rovnice se stávají jednoduššími. Například Newtonův vzorec pro výpočet přitažlivosti mezi dvěma kusy hmoty m1 a m2  nebude mít ve jmenovateli druhou mocninu vzdálenosti r, nýbrž jen první (obr. 11). Samozřejmě, že nastolení důležitosti kvadratického prostoru nabídne fyzice další práci - změní se i vztah mezi jednotkami ve zmíněném vzorci. Přitom část dosavadní fyziky neztratí svou potřebnost; zpochybňuji však její platnost.

Obr.11

       Ocejchování kvadratických os nevyžaduje výpočty. Ačkoliv jsou celá čísla na ose rozmístěna nelineárně, lze geometrickou konstrukci vyřešit kružítkem a pravítkem (obr. 12).

Obr.12

        5. Occamova břitva

        Lineární spojitý prostor vyžaduje iracionální čísla. Přepočet Pythagorovou větou z 2D do 1D vnáší iracionální vyjádření délek 1D objektů. Problém nesouměřitelnosti znesnadňuje práci vědy, chápání Vesmíru a tím i celé lidské existence.

       Geometrie kvadratického spojitého prostoru používá jen racionální čísla - celá i necelá i záporná. Při výpočtu jednorozměrné vlastnosti dvojrozměrného objektu je výsledek racionální.

       Pokud nepřijmeme kvadratický prostor za skutečnost našeho života, pak čím se stane naše dosavadní neznalost? Zůstane jen omylem? Ale jsou i další pomůcky k rozhodnutí.

      Nechť se William Occam, dnes už bájný, nerozzlobí a svou zbraň použije jen vůči našim názorům.

      6. Srovnání

Prostor                                                    Lineární                                                    Kvadratický

délka 1D                                        racionální nebo iracionální                              racionální

hodnověrnost                                  tradice od Pythagora                              smyslová informace

matematizovatelnost                až po dohodě o nových číslech                            splňuje

řád rovnic                                              kvadratické                                                    lineární

        7. Závěr

       Dějiny vědy trochu znevažují staré Egypťany a Indy, vždyť oni měli jen rovnice 32 + 42 = 52 případně 52 + 122  = 132. Teprve Evropan Pythagoras určil platnost Pythagorovy věty všem pravoúhlým trojúhelníkům. Tento můj text však obdivuje vědeckou opatrnost asijského a afrického národa ve starověku. Někteří lidé tvrdí, že vývoj civilizace před tisíciletími šel shora dolů, že lidstvo informace především ztrácelo. Pythagorova věta je sice nutná, ovšem její nevyvážené zdůrazňování brání dalším pohledům na skutečnost prostoru ve Vesmíru.

       Nová možnost představuje prostor právě takový, jaký nám znázorňuje zrak i sluch. Žádný Euklidův prostor za ním není!

       Kdo protlačí tento názor? Lidé, kteří užívají vyšší matematiku s iracionálními čísly, budou mít nadále pravdu. Pracují s Euklidovým prostorem a nebudou svou matematiku měnit. Ale Euklidův prostor není našim světem. Fyzika sama sebe zpochybní, pokud ze dvou možností nevybere tu jednodušší, tu lépe matematizovatelnou.

       Tyto názory přisvědčují těm, kteří tvrdili: smyslové zážitky dávají vzniknout tělesům!

- pokračování -

(c)2008 ing. Bohumír Tichánek