Geometrie vesmírného prostoru jinak - (1.)

       Budově přisuzujeme za nejdůležitější součást její střechu. Nejvíc trpí podnebím a její zničení pak poškodí celý dům. Jenže ve skutečnosti jsou důležitější základy domu. Ty se však málokdy bortí, takže si jejich důležitost neuvědomíme. Varování před stavěním na písku jsme vzali za své již dávno; již na ně ani nemyslíme. Domy staví specialisté. Těmi základy v oboru fyziky je prostor (obr 1a, b). Matematika i geometrie může používat různých matematických prostorů a postupů podle libosti - nemusí souviset s vesmírnou skutečností. Naopak fyzika ověřuje své názory experimenty. Dbá skutečnosti a tím bývají její výsledky pro svět velmi důležité. Časoprostor podle Minkowského má dvě složky; z nich prostor můžeme zkoumat snadněji, než čas. Euklidův prostor byl popsaný již před tisíciletími, kdežto až ve 20. století fyzika našla závislost času na rychlosti pohybu. Předkládám výhrady vůči dlouhodobému názoru na geometrii fyzikálního prostoru. Nabídnu jinou možnost.

1a) Neeuklidovský prostor

1b) Neeuklidovský prostor

       2. Pythagorova věta

       Délku úhlopříčky čtverce můžeme počítat Pythagorovou větou ze zadané délky strany trvale; nikdy neskončit (obr. 2). Ani nejrychlejší počítač se výsledku nepřiblíží. Abychom mohli nějak určit délku úhlopříčky čtverce, zaokrouhlujeme výsledek na několik desetinných míst. Smiřujeme se s chybou; zanedbáme ji.

2. Úhlopříčka Pythagorovou větou

       Považuji za správné, za nejlepší, moci zadat práci klempířovi tímto způsobem. Vyrobte čtverec o straně 1 m, a pro kontrolu - jeho úhlopříčka bude tolik a tolik. Například bych mu rád a bez obav řekl: Jeho úhlopříčka bude přesně 1,4 metru. A to bez zaokrouhlení. Nejsem spokojen s poznáním světa, když nedovedeme zdůvodnit, proč se přepočet Pythagorovou větou nedaří. Zadám-li například 1,41 metru, pak klempíř možná ani neví, že údaj je zaokrouhlený. Skutečně to nikdy lépe nepůjde?

       Konstruktér musí předem ohlídat, aby si klempíř nerval vztekem vlasy. Stranu čtverce výroba dodržela s přesností lepší než desetina milimetru, a přece v úhlopříčce 4 mm přebývají. Čtverec o straně 1,000 metru má úhlopříčku délky 1,414 metru. A žádných 1,41 či 1,410 metru.

       Klid, konstruktér přece neudává všechny rozměry výrobku a zadává i toleranci. Tento vymyšlený příklad samozřejmě není příčinou mých snah. Nýbrž mi jde o poznání světa. Horolezci lezou na vrcholy hor proto, že ty hory jsou. Podobně zvláštnost ve výpočtech délek světa se snažím prohlédnout proto, že je. Nejprve si mužové hráli s rozkladem světla do barev duhy. Až později se ukázalo, že bylo prospěšné prostudovat způsob průchodu světla sklem. Že lze vyrobit nejen okenní tabuli, ale i optický dalekohled a mikroskop. Objevit měsíční krátery a bacily.

       Popisovaný rozpor je problémem méně pro techniku a více pro filosofii či snad pro nauky o vytvoření světa. Hledání však patří exaktním oborům - fyzice, matematice.

      Matematika

      Rozlišujme důsledně, ve kterém oboru vědy prostor uvažujeme. Zda v matematice nebo ve fyzice. Obrátím-li se s nějakými názory ohledně iracionálních čísel na matematika, bude můj přístup poměřovat svými postupy. Ty dávají prospěšné výsledky. Matematika popisuje prostor reálnými čísly. Zahrnují jak racionální (např. 7 nebo 5,64 nebo 1/8), tak iracionální čísla (pí nebo odmocnina ze dvou nebo e, což je základ přirozených logaritmů).

      Nenaměříme délku úhlopříčky jednotkového čtverce ve shodě s výpočtem. Pro stranu a = 1 sděluje Pythagorova věta u = odmocnina ze 2. Výsledkem může být 1 nebo 1,4 nebo 1,41 nebo 1,414 atd. (obr. 3). Podle požadované nepřesnosti využijeme jen potřebný počet desetinných míst. Sleduji myšlenkový postup, nikoliv měření délky posuvkou nebo laserem.

3. Rostoucí vzdálenost

       Protože iracionální čísla jsou oporou vyšší matematiky, stěží matematik porozumí mým pochybnostem. Jestliže získává výsledky, pak by mělo být vše v pořádku. Souhlasím s matematikovým názorem. Je určený matematickými postupy a k tomu nemusí být příslušný Euklidův prostor provedený nikde ve Vesmíru. Matematika obohacená o iracionální čísla dává výsledky, ale přitom nemusí být skutečností fyziky.

       Fyzika

       Fyzika bádá nad vesmírnými záležitostmi. Tudíž ověřování experimenty je nutné, soulad s nimi je žádoucí. Fyzika pracuje s prostory, o kterých si nejsme jistí, zda vůbec můžou být či jsou skutečné. Uvažuje prostory čtyřrozměrné (4D) či 5D a ještě více rozměrné, i když je možná všechny ve Vesmíru nenajdeme (obr. 4). Nevnímané rozměry by mohly být nějak svinuté, nějak skryté, a protože se používají jen ve výpočtech, k rozporu nedochází.

4a) 4D krychle

4b) 4D krychle

4c) 4D krychle

4d) 4D krychle

        Matematika nepotřebuje posuzovat, zda její používané prostory ve Vesmíru existují. Odpovídající rovnice vyššího řádu lze využívat, ale našemu vnímání stále zůstává otázka - kam směrovat čtvrtou kolmici v našem prostoru? Má být také posunutá o 90° oproti ostatním třem kolmicím. To nám dosud ve Vesmíru nikdo neukázal.

        K čemu směřuji? Tak jako fyzika svými výpočty pracuje s vícerozměrnými prostory, stejně tak pracuje s Euklidovým prostorem. V obou případech nemáme záruku, že takový prostor existuje. Nejistota existence Euklidova prostoru je předmětem tohoto uvažování. Jak 11D, tak Euklidův trojrozměrný prostor pouze předpokládáme. Zrakem však zjišťujeme prostor jiný, stlačený perspektivou. Ovšem to je pouhý smyslový zážitek.

       Zkouším prověřit 3D Euklidův prostor tam, kde výpočet nedává racionální řešení. Naprosto si nemyslím, že by matematika selhávala. Ta řeší bez chyby. Zaručuje, že výpočet desetinného vyjádření iracionálního čísla bude vždy bez konce.

       Prostor k pokroku hledám v geometrii.

       Geometrie

       V Euklidově geometrickém prostoru vyjadřujeme 1D délku jedním a jindy druhým obvyklým způsobem. Změříme stranu čtverce, zadáme do výpočtu a pak je výsledkem úhlopříčka vždy iracionální. Nebo naopak (obr. 5). Délky strany a úhlopříčky jsou nesouměřitelné, vyjádřené buď racionálním nebo iracionálním číslem. Tato mnohost vede k pochybnosti, zda je to v úplném pořádku. Váhám nad prostorem, ve kterém používáme dvojí vzdálenosti. Je to konečná pravda? Bylo by lepší, kdyby této zdvojenosti nebylo. Pěkné by bylo vyjadřování délek výhradně racionálními čísly.

5. Nesouměřitelnost

        O složitostech je známo: "Velké objevy ve fyzice jsou proto velké, že redukují počet postulátů potřebných na popis světa na nejmenší počet. To je při hledání nových poznatků nejvlastnější funkce vědy." (Július Krempaský: Vesmírne metamorfózy. Vyd. Smena 1989, strana 16).

       Zde však místo velkých objevů připomínám nutnost pochyb nad složitostí. Nad nutností používat dvojí délky 1D prostoru.

       Podpora mé nedůvěry

       Na internetové adrese "Neviditelny pes" v sekci vědy byla 15.10.2002 veřejná diskuse k Pythagorově větě (Vojtěch Hála). Ona se netýká jen čtverců, ale i některých dalších obrazců nad odvěsnami a nad přeponou pravoúhlého trojúhelníka (obr. 6).

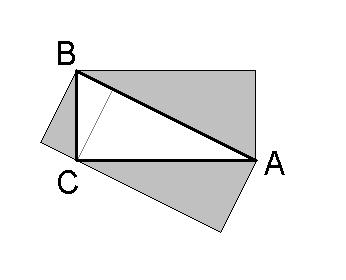
6. Pythagorova věta trojúhelníků

       Z diskuse vybírám jeden ze zveřejněných příspěvků:

       Důkaz je platný, maximálně bychom se mohli bavit o jeho exaktnosti - závěr důkazu je postaven na optické shodě součtu obsahů trojúhelníků nad odvěsnami, když se přemístí do trojúhelníka původního. Jinými slovy, my tu platnost toho součtu "vidíme", a to může být v obecném případě ošemetné. Stačí malá modifikace úlohy, např. kreslit trojúhelníky na dostatečně velké kulové ploše, a už bychom s tím odsouhlasením optické shody váhali, a to dokonce i v případě, kdy by Pythagorova věta pro ten sférický pravoúhlý trojúhelník platila (jakože neplatí). Tedy z ryze formálního hlediska je slabým místem důkazu pouze ten poslední krok, kdy důkaz ukončíme tvrzením, že "je to vidět". Pavel Brož

        Dodávám - tak jako nelze posuzovat odhadem shodnost ploch na povrchu koule, nedovolím si to ani v rovině (obr. 7). I tady dbám výpočetního prověření. To však nekončí. Převod z 2D prostoru do 1D prostoru se řeší zavedením dohodnutého druhu iracionální délky a nebo zaokrouhlením.

7. Pythagorova věta v síti

        Připadá mi paradoxní, že odmocnina ze dvou je současně číslem - iracionálním, a současně pokynem k hledání čísla: hledej číslo x, které násobené samo sebou dává dvě! Tedy v rovnici x*x = 2 (obr. 8)

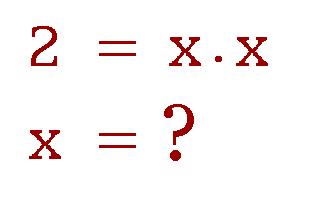
8. Hledání odmocniny

       Nesnáz s Popperem

       Při hledání souvislostí iracionálních čísel v geometrii pátrám po jiném prostoru. Zajímavý je názor Ernesta Macha, dávno zesnulého německého fyzika původem z Moravy. Měl za to, že zvláště fyzika získá největších vysvětlení od biologie, a to analýzou smyslových počitků. Vycházel z názoru,  že objektem vědy jsou komplexy počitků, které nemají objektivní příčinu. I v kvantové  mechanice lze uvažovat Machovým způsobem.

        Matematika vznikla ze smyslových zážitků. I když až jejich abstrakcí. Fyzikální poznatek o teplotě hrnku s vřelou vodou lze někdy zjistit i bez přemýšlení, kdežto zjistit počet hrnků vyžaduje abstrahovat.

        Zjišťuji jakousi nesnáz pro závěry filosofa K. Poppera. Na jedné straně bývají smyslové zážitky podrobené chybám. Hledíme na obraz rovnoběžek, ale máme pocit, že jsou to různoběžky (obr. 9). Změřením se chybný názor vyvrátí. Vliv šálivé podrobnosti u každého čtverce lze pochopit a zneškodnit (obr. 10). Rozmístění rohových čtverečků zdánlivě zkracovalo délku některých stran čtverců.

9. Různoběžky

10. Rovnoběžky

       Slyšíme zvuk z prostoru mezi reprobednami, takže tam zdroj zvuku musí být - věděl by se zavřenýma očima dávno odešlý Mozart. Přece je jinde! Exaktní poznání často opravuje chybně vyhodnocené zážitky smyslů. Ale vyvrátit tyto smyslové poznatky nelze. Vždyť dvojice uší s mozkem prověří zdroje signálu a pak upřímně informuje naše vědomí o příchodu zvuku z prostoru mezi reprobednami. Příště může posluchač hodnotit směrování zdroje opět nesprávně, pokud budou falešné reprobedny schválně přichystané k jeho zmýlení.

       Nepodceňuji prostor, vědou opomíjený, obsažený v našich smyslových zážitcích. Na ně může člověk přísahat, že je má. Smyslové zážitky jsou ovšem nevědecké tím, že jsou snad nevyvratitelné! Nejen každodenní zážitky sluchu, zraku, čichu, chutě a hmatu, ale i jejich pokřivené odvozeniny. Poživačům drog se zrakové zážitky můžou prohýbat. Popisem skutečnosti nejsou, ale zřejmě jsou nevyvratitelnými (nefalsifikovatelnými) zdroji informací. Věda opravuje svými vysvětleními až chápání zážitků. Vidí-li opilec bílé myši, pak mu nikdo nevyvrátí, že vidí bílé myši. A přitom může souhlasit, že nejsou skutečné. Smyslové poznatky jsou vysvětlitelné, ale pochybuji, že by byly vyvratitelné. Může dojít k záměně, spící člověk obvykle bývá přesvědčený o skutečnosti svého snového prožívání.

      Filosof Karl Raimund Popper poučil - předpokladem vědeckého pokroku je vyvratitelnost přijímaných poznatků. Nevyvratitelné názory věda nejen odmítá, ale někdy jimi lidé i opovrhují. Jenže naše nevyvratitelné smyslové zážitky jsou základem veškerého poznání.

- pokračování -